1. Узагальнення поняття вектора. векторний простір
2. Що таке лінійне перетворення?

На двох найближчих уроках я коротко розкажу вам ще про одне розділі вищої алгебри , Який стосується лінійних перетворень ... і тут відразу, зауважте, напрошується додати «перетворень чогось». Тема велика, тема цікава, і моя скромна задача полягає в тому, щоб у доступній формі донести до читача її основи. У зв'язку з цим стаття буде присвячена не тільки абстрактним алгебраїчним питань, але і наповнена багатим геометричним змістом. Крім того, сьогодні ми узагальнимо таке важливе поняття як вектор, який має до цього змістом лише приватне ставлення.

Узагальнення поняття вектора. векторний простір

Очікування страти гірше самої кари і тому краще відразу відчути льодовий холодок справжньою алгебри =) Почнемо з обіцяного розбору польотів, а саме з поняття вектора. Давайте згадаємо, що ми про неї знаємо. Паличка зі стрілочкою, знайома ще зі школи. У вищій математиці ця паличка «піднялася» до вільного вектора площині і простору. Добре…. Далі слово «вектор» зустрілося нам в ході вивчення матриць . Так, наприклад, матрицю «один на два» 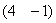ми називаємо вектором-рядком, а матрицю «три на один» - вектором-стовпцем. Це вектори? Так, це вектори! Причому ці вектори самі по собі не мають ніякого відношення до геометрії. У своїх статтях з алгебри я неодноразово наголошував, що «даний вектор потрібно розуміти в алгебраїчному сенсі» і на уроці про ранзі матриці привів коротку теоретичну довідку з цього приводу: вектор - це упорядкований набір чисел 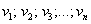(зазвичай дійсних) ... і далі по тексту. А ось це вже ближче до істини: тут, скажімо, двовимірний вектор 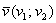розуміється саме як упорядкована пара чисел, яку, зокрема можна інтерпретувати, як координати геометричного вектора. Або як рішення системи лінійних рівнянь (див., Наприклад, статтю про однорідних системах ). Або ще як-небудь.

Але і це випадковість! Насправді в певному контексті векторами є матриці, многочлени, функції і т.д. ... і навіть наші «звичайні» дійсні числа ! А чому ні? Будь ласка: безліч векторів (ніяких геометричних асоціацій!), що мають в наборі одне дійсне число .

Так що ж таке вектор? Що об'єднує всі ці випадки?

Припустимо, що для всіх елементів деякої множини визначені операції їх складання 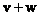і множення на скаляр 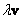, Причому результати цих операцій (отримані елементи) теж належать даній безлічі. Якщо при цьому виконані наступні вісім аксіом (див. за посиланням), то розглядаються елементи називаються векторами (ніяких асоціацій !!), а все їх безліч - векторним або лінійним простором

Зверніть увагу на позначення: абстрактний вектор найчастіше записують жирної буквою - щоб не виникало плутанини з різними «конкретними» векторами. Для векторного простору стандартно використовується буква .

Отже, які б «приватні сімейства» векторів ми не взяли (геометричні, матричні, строкові і т.д.) - для кожної з цих алгебраїчних структур справедливо наступне:

- всі елементи розглянутого безлічі можна складати і множити на скаляр (далі працюємо з дійсними числами), причому результати цих операцій теж належать даній безлічі.

- для операцій додавання і множення виконані аксіоми векторного простору .

І тут слід зазначити, що терміни «складання» і «множення» теж носять загальний символічний сенс - в залежності від природи того чи іншого векторного простору ці операції визначаються по-різному.

В курсі лінійної алгебри проводиться скрупульозна перевірка різних множин на предмет того, чи утворюють вони лінійний простір. І якщо вдасться визначити додавання і множення на скаляр ведмедів на велосипеді і довести для даних операцій виконання зазначених 8 аксіом, то векторами будуть і ці об'єкти =)

А тепер до основної теми уроку:

Що таке лінійне перетворення?

Якщо в лінійному просторі 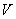кожному вектору 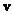по деякому правилу 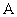поставлений у відповідність вектор 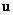цього ж простору, то кажуть, що в даному просторі задана векторна функція векторного аргументу: 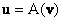(щоб уникнути різночитань з іншими математичними записами дужки нерідко опускають: ).

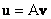Ця функція називається лінійним перетворенням, якщо для неї виконані горезвісні властивості лінійності, з якими ви ще не раз зіткнетеся в ході вивчення вищої математики:

,
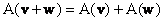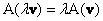, де 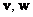- довільні вектори даного простору, а - дійсне число.

Лінійне перетворення також називають лінійним оператором.

Наступний приклад обріс не тільки бородою, але і волоссям на спині: розглянемо лінійне простір векторів-рядків виду 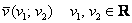, В якому визначені операція додавання і множення вектора на число .

Ніякої геометрії !!! - то, що я сформулював в статті про ранзі матриці , називається
-мірним арифметичним векторним простором, і зараз ми маємо справу з приватним арифметичним простором розмірності 2.

Доведемо, що функція векторного аргументу 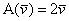є лінійним перетворенням. Доказ складається в перевірці властивостей лінійності:

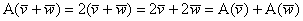
Тут ми скористалися дистрибутивну множення на скаляр щодо додавання векторів (одна з аксіом векторного простору )

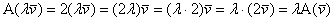
А тут - аксіомою асоціативності множення на скаляр, коммутативностью (перестановки) самих дійсних чисел (аксіома поля ) І знову тієї ж аксіомою асоціативності.

Читачам, яким належить вивчати теорію вищої алгебри , Слід звикнути до таких доказів. Нещадно формально, але, як сказали б древні римляни, Dura algebra sed algebra =)

Таким чином, 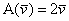- це лінійне перетворення.

Зрозуміло, далеко не всякий оператор є лінійним, і в інших джерелах інформації можна знайти безліч прикладів, як на вдалу, так і невдалу перевірку різних перетворень на лінійність. І зі строгістю доказів на практиці зазвичай все простіше, ... хоча, тут від викладача залежить - і по-хорошому, в математиці ще потрібно обгрунтувати, чому «нуль НЕ дорівнює одиниці».

Ну а зараз ми спускаємося на землю грішну і переходимо до геометричного змісту лінійних перетворень. нехай 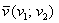- це безліч геометричних векторів площини. Для простоти розглянемо звичний ортонормованій базис і прямокутну систему координат .

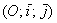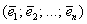Якщо заданий будь-якої базис, то лінійне перетворення зручніше представити в матричному вигляді. Як записати оператор у вигляді матриці ? На цей рахунок існує загальне правило: щоб записати матрицю лінійного перетворення в -мірному базисі потрібно послідовно і строго по порядку застосовувати даний оператор до базисних векторах, а результати заносити в стовпці матриці (зліва направо).

Наш випадок проста: спочатку застосуємо лінійне перетворення 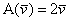до першого базисного вектора: і запишемо результат в 1-й стовпець: 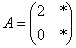. Потім «обробляємо» 2-й орт : 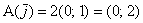і заносимо отримані координати в 2-й стовпець:

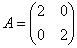- матриця лінійного перетворення 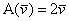в базисі .

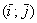Протестуємо побудовану матрицю за допомогою вектора 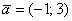. Для цього «укладемо» його координати в вектор-стовпець і виконаємо наступне матричне множення :
- в результаті «на виході» отримані координати вектора 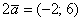, Що і було потрібно перевірити.

Оскільки будь-яка точка площині однозначно визначається її радіус-вектором ( 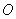- початок координат), то матриця перетворення, по суті, може бути застосована і до координат точок. І далі для простоти я буду говорити, що, наприклад, точка :
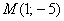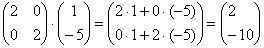- перейшла в точку .

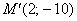Напевно, всі вже зрозуміли, що робить цей оператор. Подумки уявіть довільний трикутник на площині. Після застосування розглянутого лінійного перетворення даний трикутник збільшиться в два рази. Такі трикутники (які мають рівні відповідні кути), як багато хто пам'ятає зі школи, називаються подібними. Та й сам оператор носить таку ж назву:

лінійне перетворення 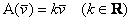називається перетворенням подібності або Гомотетія, причому:

- якщо 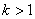, То мова йде про однорідному розтягуванні (збільшенні) об'єктів площині в 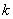раз;
- якщо 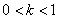- то про стиснення (зменшення) в 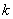раз;
- якщо , То перетворення тотожне (нічого не змінює).
І якщо по модулю менше нуля, то додатково до розтягування / стиснення / незмінності вектори змінюють напрямок, а точки відображаються симетрично відносно початку координат.

при 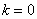має місце так зване нульове перетворення.

Слід зазначити, що на прикладному і «любительському» рівні лінійні перетворення найчастіше якраз і асоціюються саме з геометричними перетвореннями. Розглянемо ще кілька популярних прикладів по темі, і, щоб урізноманітнити сірі геометричні будні, подумки намалюємо на координатної площині котячу морду. Можна і не подумки =)

... Представили? Намалювали? Відмінно!

перетворення 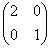розтягує об'єкти площині у напрямку вектора 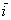(горизонталі) в 2 рази, після чого кіт Леопольд радує нас своєю широкою-широкою посмішкою!

... хоча у багатьох, напевно, не кіт ... та й не факт, що з посмішкою ... - як то кажуть, у кожного в голові своя морда =)

І справді, перетворимо точку :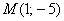
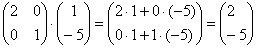- «іксів» координата збільшилася в 2 рази, а «ігрековая» - не змінилася.

перетворення 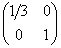стисне кота по горизонталі в 3 рази. Бажаючі можуть по ходу пояснень приготувати м'ясорубку тестувати для розглянутих матриць різні вектори і точки. Читачам хоч у якійсь мірі навичками матричного множення не складе особливих труднощів робити це усно.

перетворення витягне все ненульові об'єкти площині у напрямку вектора 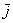(по вертикалі) в півтора рази. Це буде дуже здивований кіт ....

Додаткові знаки «мінус» приведуть до дзеркального відображення об'єктів (щодо осі ординат або початку координат).

- образно кажучи, «щелепу наліво, лоб направо». Це перетворення називається перекосом або зрушенням площині в напрямку вектора 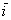(в даному випадку).

- дане перетворення повертає вектори системи 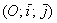проти годинникової стрілки на кут .

І, нарешті, вінчає всі ці метаморфози ще один кошлатий приклад:
перетворення переводить одиничний квадрат з вершинами 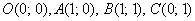в паралелограм з вершинами .

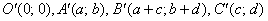А тут вже справа випадку - може вийти, як кімната сміху, так і кімната страху - залежить від того чи іншого перетворення.

З вищесказаного неважко зрозуміти, що в базисі 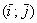будь-який квадратної матриці «Два на два» відповідає деякий лінійне перетворення, і навпаки будь-якому лінійному перетворенню відповідає своя матриця «два на два». І цей факт справедливий взагалі для будь-якого афінного базису 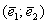, Причому один і той же лінійне перетворення в різних базисах матиме в загальному випадку різні матриці (що випливає з самого принципу формування цих матриць).

За аналогічною схемою можна розглянути вектори 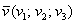нашого тривимірного простору, з тією відмінністю, що перетворень буде більше, перетворення будуть веселіше. І, зрозуміло, лінійні перетворення «працюють» в векторних просторах бОльшей розмірності, однак там вони вже далекі від геометрії.

розминаємося:

приклад 1

В деякому афінному базисі задано лінійне перетворення 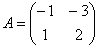. Знайти образ точки 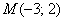. Використовуючи зворотне перетворення, виконати перевірку.

Рішення: потихеньку навантажую вас термінологією: образ - це те, що повинно вийти в результаті перетворення. В даному випадку, очевидно, повинна вийти деяка точка . вихідна точка , Відповідно, є прообразом.

! Сподіваюся, всі розуміють, що штрихи в даному контексті не мають ніякого відношення до похідним .

Образи векторів і точок ми вже неодноразово знаходили вище: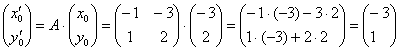

Таким чином, лінійне перетворення перевело точку в ціль .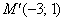

Тепер знайдемо матрицю зворотного перетворення, яке перетворює образи векторів і точок назад в їх прообрази. Для цього запишемо найпростіше матричне рівняння 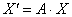(де 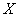- координатний стовпець прообразів, а 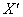- образів) і для його дозволу щодо 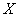помножимо обидві частини на зворотний матрицю 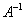зліва: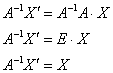

«Розгорнемо» рівняння в звичному порядку: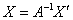

Обернену матрицю можна знайти через алгебраїчні доповнення або методом Гаусса-Жордана , Але тут я рекомендую перший спосіб, оскільки він дозволить швидко з'ясувати, а чи існує матриця взагалі.

Заряджаємо стандартний алгоритм. спочатку обчислимо визначник :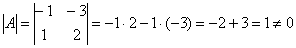
, Значить, матриця лінійного перетворення оборотна. Зі змістовної точки зору це означає, що зворотне лінійне перетворення існує і задається він докладно матрицею .

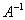Тут і далі я не буду детально розписувати процес знаходження оберненої матриці . Отже, в результаті стандартних дій знаходимо 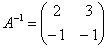і з'ясовуємо, на що перетвориться знайдена точка :

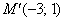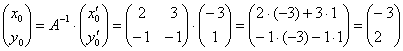- отримані координати вихідної точки , Що і було потрібно перевірити.

відповідь: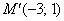

Слід зазначити, що зворотне перетворення можна здійснити далеко не завжди. Так буває, наприклад, при проектуванні векторів на координатні осі або при тривіальному нульовому перетворенні. У таких випадках визначник матриці прямого оператора дорівнює нулю 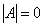і оберненої матриці 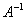не існує.

Творче завдання для самостійного рішення:

приклад 2

В результаті застосування оператора 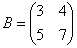в деякому базисі отримані образи . Знайти прообрази даних векторів.

Короткий рішення і відповідь в кінці уроку. Зверніть увагу, що формулювання даного завдання зовсім не стверджує, що мова йде саме про геометричні вектори. Як воно, власне, і буває в більшості типових завдань, які для повного комфорту оформляються малозрозумілою клинописом:

приклад 3

Дано два лінійних перетворення: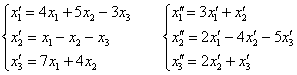

Спокійно, спокійно, зараз у всьому розберемося ...

Засобами матричного обчислення знайти перетворення, що виражає 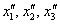через .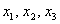

Рішення: і як раз перше, що тут можна сказати - це відсутність інформації про характер векторів . Відомо тільки, що вони задані в деякому базисі, бо матриця лінійного перетворення НЕ МОЖЕ існувати без базису (тому що вона породжується базисними векторами). Сам базис нам теж ніхто не знає, але для вирішення завдання інформація про нього і не потрібна.

Проте, для більшого розуміння припустимо, що всі справи відбуваються у звичайній декартовій системі координат 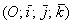. І, щоб не уславитися шкуродерками, я розгляну 3D-модель кота Леопольда =)

Запишемо матрицю лівого перетворення: 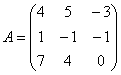. Дане перетворення переводить вектори 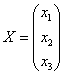в образи . Систему, до речі, зручніше переписати у вигляді вже знайомого матричного рівняння :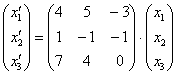
або, якщо коротше: .

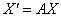Даний оператор певним чином перетворює все вектори (а значить і точки) простору. Геометрично це означає, що кіт Леопольд, виявляється, наприклад, сплющеним (не знаю, не перевіряв).

Тепер УВАЖНО записуємо матрицю другого перетворення: 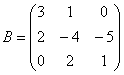(тут існує чималий ризик поставити нуль не там де потрібно). Дане перетворення переводить вектори 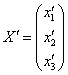в образи 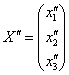, В результаті чого «сплющений кіт», скажімо, розтягується вздовж якоїсь площині.

Аналогічно - запишемо перетворення в матричному вигляді: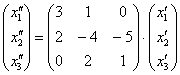
або: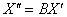

За умовою, потрібно знайти результуюче (композиційне) перетворення, яке нам відразу дасть «сплющенного і розтягнутого Леопольда». підставами 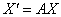в рівняння :

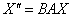
Все виявилося до неподобства просто - головне, матриці помножити на правильному порядку. Обчислимо матрицю композиційного перетворення: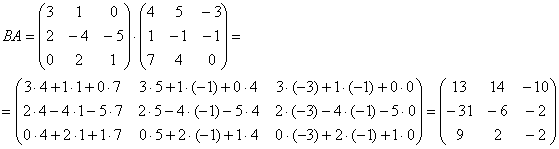

Якщо ви забули саме матричне множення, зверніться до статті Властивості матричних операцій , Де я докладно розібрав цей випадок.

В результаті: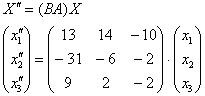

Здійснимо матричне множення в правій частині: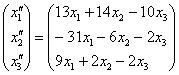

Дві матриці рівні, якщо рівні їх відповідні елементи. Таким чином, підсумкове перетворення, що виражає координати векторів-образів 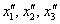через координати векторів-прообразів 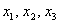, Запишеться у вигляді такої системи: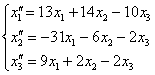

Виконаємо перевірку. Для цього підставимо рівняння 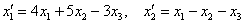, лівої системи (див. умову) в праву частину кожного рівняння 2-й системи:

Що й треба було перевірити.

Цей спосіб, до речі, можна було б ризикнути взяти і за основою, якби підсумкове перетворення не було потрібно знайти засобами матричного числення

відповідь:

Як користуватися цією системою? Дуже просто - беремо наприклад, вектор 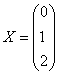і тупо підставляємо його координати:
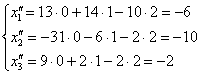- таким чином, він перетворився в вектор .

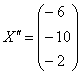Більш академічний спосіб - використання матричного рівняння .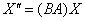

Ентузіасти можуть змоделювати деформацію кота Леопольда за допомогою спеціалізованого програмного забезпечення і відправити мені картинку, яку я обов'язково опублікую. Мені і самому цікаво, що ж там з ним насправді сталося =)

У тому випадка, если нужно «повернути кота до первісного вигляд», слід найти зворотнього матриці результуюча превращение і скористатися рівнянням .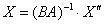

«Плоский» випадок для самостійного рішення:

приклад 4

Дано два лінійних перетворення в деякому базисі: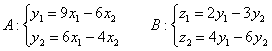

Знайти образ вектора двома способами:

1) шляхом послідовного застосування перетворень 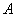и ;
2) за допомогою композиційного оператора, що виражає координати через .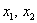

Була велика спокуса вас запитати, але все ж я утримався. Однак на практиці потрібно мати на увазі наступне:

- системи запросто можуть бути переставлені місцями;

- умову задачі може вимагати висловити 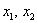через 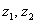і тоді буде потрібно додатково знаходити зворотну матрицю результуючого перетворення;

У зв'язку з цим дуже важливо РОЗІБРАТИСЯ в суті завдання, і якщо щось залишилося недопонятом, обов'язково перечитайте пояснення ще раз - не зайвим буде навіть помалювати.

А зараз переходимо до питання, який назрівав протягом всього уроку:

На початку статті ми з'ясували походження матриці лінійного перетворення на прикладі оператора 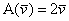і ортонормированного базису 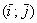. Нагадую: для того, щоб записати матрицю лінійного оператора в будь-якому базисі, потрібно строго по порядку подіяти цим оператором на базисні вектори і отримані координати занести в стовпці матриці (зліва направо). В результаті «обробки» векторів нами була складена матриця 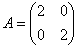даного лінійного перетворення в даному базисі.

Але ж на «шкільному» базисі світло клином не зійшовся! Ніщо нам не заважає перейти до довільного базису , Де це ж лінійне перетворення, очевидно, виявиться інший матрицею. Але сам-то оператор не зміниться - він буде як і раніше збільшувати вектори площині в 2 рази. Таким чином, справедливо наступне твердження, яке по суті вже було озвучено раніше:

Одне і те ж лінійне перетворення в різних базисах в загальному випадку має РІЗНІ матриці.

І такі два завдання як раз присвячені цьому питанню:

приклад 5

В базисі 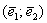задано лінійне перетворення 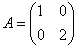. Знайти матрицю даного перетворення в базисі 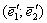, если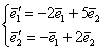

Рішення: в умові завдання знову нічого не сказано про характер векторів, але для наочності припустимо, що дані базиси є аффінним базисами площині . Як помітили уважні читачі, запропоноване лінійне перетворення витягує всі ненульові об'єкти площині в напрямку координатного вектора 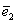в 2 рази, і наше завдання полягає в тому, щоб записати матрицю 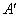цього ж перетворення в новому базисі 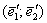. Для вирішення цього питання існує спеціальна формула:

, де 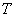- матриця переходу від базису 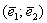до базису .

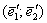Складається вона просто: беремо вектор 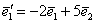і «укладаємо» коефіцієнти його розкладання (увага!) в 1-й стовпець матриці: 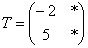. Потім розглядаємо вектор 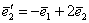і заносимо коефіцієнти його розкладання в 2-й стовпець:

Увага! Базисні вектори, в даному випадку вектори 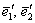, Слід «перебирати» строго по порядку!

Інша справа техніки. знаходимо зворотний матрицю :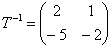

Твір, добуток: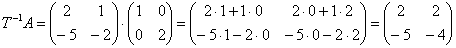

І, нарешті, матрицю розглянутого лінійного перетворення в новому базисі: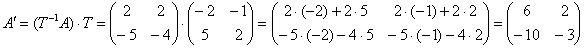

Користуючись асоціативністю матричного множення , Можна було спочатку знайти 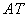, а потім , Але, в общем-то, це вже несуттєві деталі.

відповідь: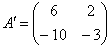

Ще раз повторимо зміст завдання: саме лінійне перетворення залишається такою - воно як і раніше розтягує ненульові об'єкти площині уздовж «старого» вектора 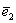в 2 рази і не деформує їх в напрямку вектора 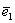, Але в новому базисі матриця даного перетворення вже інша. І ви бачите її у відповіді.

Очевидно, що знайдена матриця 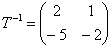задає зворотне перетворення, тобто висловлює старі базисні вектори через нові. Акуратно «транспоніруем» стовпці матриці в коефіцієнти відповідної системи: 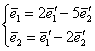. Таким чином, при бажанні завжди можна повернутися до старого базису: 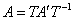. Зворотній формула випливає з простих логічних міркувань, але її можна вивести і формально - дозволивши матричне рівняння 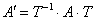относительно .

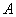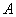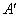іноді матриці и називають подібними.

Який базис зручніше? Звичайно ж, вихідний, який задається матрицею 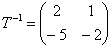- він відразу дозволяє з'ясувати характер лінійного перетворення. І що це за такий цікавий базис, і як отримати цю матрицю іншим способом, ви дізнаєтеся на уроці про власних векторах .

Тривимірний випадок для самостійного рішення:

приклад 6

Знайти матрицю лінійного перетворення в базисі 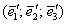, де , , 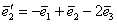, 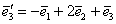Якщо вона задана в базисі .

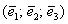Будь ласка, не плутайте це завдання з Прикладом № 3 - по першій оглядці тут теж якісь схожі рівності, теж штрихи, але сенс скоєно інший. Якщо там йшлося про двох лінійних перетвореннях і взаємозв'язку координат векторів, то тут - про одне й те ж перетворенні і взаємозв'язку векторів двох базисів.

Короткий рішення і відповідь зовсім поруч.

І в завершенні уроку повернемося до двовимірному нагоди і матрицями «два на два». Здавалося б, з геометричної точки зору ці матриці задають лінійні перетворення площині і розмова закінчена. Але насправді це не так - у матриць є й інший геометричний сенс, з яким можна ознайомитися на уроці Перехід до нового базису . Спочатку я хотів включити пару відповідних прикладів в цю статтю, але трохи пізніше вирішив, що матеріал буде доречніше опублікувати в розділі аналітичної геометрії .

Ну і звичайно, не забуваємо, що розглянутий матеріал стосується не тільки геометричних векторів площини і простору, а й взагалі будь-яких векторів.

Дякую за увагу, чекаю вас на наступному, не менше цікавому уроці про власних числах і власних векторах лінійного перетворення.

Рішення і відповіді:

Автор: Ємелін Олександр

Вища математика для заочників і не тільки >>>

(Перехід на головну сторінку)