Роль статистичних розподілів в роботі трейдера
- Вступ
- 1. Генерація випадкових чисел з заданим розподілом
- 2. Оцінка параметрів розподілів, статистичні гіпотези
- 3. Підгонка розподілу
- Висновок
У житті допомагають закономірності, але не менш важливо отримувати користь з випадковості.
(Георгій Александров)
Вступ
Дана стаття є логічним продовженням моєї статті Статистичні розподілу ймовірностей в MQL5 , В якій були представлені класи для роботи з деякими статистичними теоретичними розподілами. Я знайшов необхідним спочатку створити певний фундамент у вигляді класів розподілів, щоб потім користувачеві було зручніше працювати з ними на практиці.
Тепер, коли є деяка теоретична база, я пропоную безпосередньо перейти до вибірок реальних даних і спробувати отримати деяку інформаційну користь від цієї бази. Попутно будуть висвітлюватися деякі моменти, пов'язані з математичною статистикою.
1. Генерація випадкових чисел з заданим розподілом
Але перш ніж розглядати реальні вибірки даних, є дуже важливим мати можливість отримувати деяку сукупність величин, яка мала б близьке відношення до бажаного теоретичного розподілу.
Тобто, користувач повинен лише вказати параметри розподілу, яке йому потрібно, і задати розмір вибірки. А програма (в даному випадку ієрархія класів) повинна згенерувати і вивести для подальшої роботи таку вибірку величин.
Ще одна важлива деталь полягає в тому, що згенеровані по заданому закону вибірки використовуються для перевірки різних статистичних тестів. Ця область математичної статистики - формування випадкових величин з різними законами розподілу - досить цікаве і непросте напрямок.
Для своїх цілей я скористався генератором вищої якості, який описаний в книзі Numerical Recipes: The Art of Scientific Computing [2]. Його період приблизно дорівнює 3.138 * 1057. Код на мові C досить легко було перенести в MQL5 .
Отже, я створив клас Random наступним чином:
class Random {private: ulong u, v, w; public: void Random () {randomSet (+184467440737095516); } Void randomSet (ulong j) {v = 4101842887655102017; w = 1; u = 14757395258967641292; u = j ^ v; int64 (); v = u; int64 (); w = v; int64 (); } Ulong int64 () {uint k = 4294957665; u = u * 2862933555777941757 +7046029254386353087; v ^ = v >> 17; v ^ = v << 31; v ^ = v >> 8; w = k * (w & 0xffffffff) + (w >> 32); ulong x = u ^ (u << 21); x ^ = x >> 35; x ^ = x << 4; return (x + v) ^ w; }; double doub () {return 5.42101086242752217 e- 20 * int64 (); } Uint int32 () {return (uint) int64 (); }};
Тепер можна створювати класи для величин, обраних з будь-якого розподілу.
Для прикладу розглянемо випадкову величину з нормального розподілу. Клас CNormaldev представлений так:
class CNormaldev: public Random {public: CNormaldist N; void CNormaldev () {CNormaldist Nn; setNormaldev (Nn, 18446744073709); } Void setNormaldev (CNormaldist & Nn, ulong j) {N.mu = Nn.mu; N.sig = Nn.sig; randomSet (j); } Double dev () {double u, v, x, y, q; do {u = doub (); v = 1.7156 * (doub () - 0.5); x = u - 0.449871; y = fabs (v) + 0.386595; q = pow (x, 2) + y * (0.19600 * y- 0.25472 * x); } While (q> 0.27597 && (q> 0.27846 || pow (v, 2)> - 4. * log (u) * pow (u, 2))); return N.mu + N.sig * v / u; }};
Як можна помітити, в класі є дані-член N типу CNormaldist. В оригінальному сішном коді такого зв'язку з розподілом не було. Я вважав за потрібне, щоб випадкова величина, що генерується класом (тут класом CNormaldev), мала логічну і програмну зв'язок зі своїм розподілом.
У вихідному варіанті тип Normaldev задавався так:
typedef double Doub; typedef unsigned __int64 Ullong; struct Normaldev: Ran {Doub mu, sig; Normaldev (Doub mmu, Doub ssig, Ullong i) ...}
Генерація випадкових чисел з нормального розподілу тут відбувається по методу коефіцієнта однаковості Леви.
Всі інші класи, за допомогою яких обчислюються випадкові величини з різних розподілів, знаходяться під включається файлі Random_class.mqh.
Зараз з генерацією закінчимо, а в практичній частині статті розглянемо, як можна створювати масив величин і тестувати вибірку.
2. Оцінка параметрів розподілів, статистичні гіпотези
Зрозуміло, що ми будемо досліджувати дискретні величини. Однак, на практиці, при великій кількості дискретних величин, зручніше вважати сукупність таких величин групою безперервних величин. Це стандартний підхід в математичній статистиці. Тому для їх аналізу ми можемо використовувати розподілу, описувані аналітичними формулами, пов'язаними з безперервними величинами.
Отже, давайте приступимо до процедури аналізу емпіричного розподілу .
Передбачається, що вивчається вибірка деякої генеральної сукупності, члени якої відповідають умові репрезентативності . Крім того, задовольняються вимоги до оцінок, зазначені в розділі 8.3 [9]. Числові параметри розподілу можуть бути знайдені за допомогою точкових або інтервальних методів.
2.1 Обробка вибірки за допомогою класу CExpStatistics
Спочатку з вибірки потрібно видалити так звані викиди ( outliers ) - значення ознаки, що різко відрізняються від значень ознаки у основній частині одиниць сукупності (як в більшу, так і в меншу сторону). Якогось одного універсального методу видалення викидів не існує.
Пропоную застосувати той, який був описаний С.В. Булашева в розділі 6.3 [5]. На форумі MQL4 була створена бібліотека статистичних функцій, на основі яких ми легко вирішимо поставлену задачу. При цьому, звичайно, ми звернемося до можливостей ООП і трохи її модернізуємо.
Створений клас оцінок статистичних характеристик я назвав CExpStatistics (Class of Expected Statistics).
Виглядає він приблизно так:
class CExpStatistics {private: double arr []; int N; double Parr []; int pN; void stdz (double & outArr_st [], bool A); public: void setArrays (bool A, double & Arr [], int & n); bool isProcessed; void CExpStatistics () {}; void setCExpStatistics (double & Arr []); void ZeroCheckArray (bool A); int get_arr_N (); double median (bool A); double median50 (bool A); double mean (bool A); double mean50 (bool A); double interqtlRange (bool A); double RangeCenter (bool A); double meanCenter (bool A); double expVariance (bool A); double expSampleVariance (bool A); double expStddev (bool A); double Moment (int index, bool A, int sw, double xm); double expKurtosis (bool A, double & Skewness); double censorR (bool A); int outlierDelete (); int pArrOutput (double & outArr [], bool St); void ~ CExpStatistics () {}; };
Реалізацію кожного методу можна буде детально вивчити під включається файлі ExpStatistics_class.mqh, тут я її пропускаю.
Важливе, що виконує даний клас, - це повернення очищеного від викидів масиву (Parr []), якщо звичайно викиди мали місце. Крім того, з його допомогою можна отримати деякі описові статистики вибірки і їх оцінки.
2.2 Створення гістограми для обробленої вибірки
Тепер, коли масив очищений від викидів, за його даними можна побудувати гистограмму (Розподіл частот). Вона дозволить нам візуально оцінити закон розподілу випадкової величини. Гістограма будується поетапно.
Спочатку потрібно розрахувати кількість необхідних класів. В даному контексті поняття "клас" означає угруповання, інтервал. Число класів розрахуємо за формулою Стерджеса (Sturges):
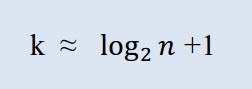
Де, k - число класів, n - чисельність сукупності.
У MQL5 варіанті формулу можна представити так:
int Sturges (int n) {double s; s = 1. + log2 (y); if (s> 15) s = 15; return (int) floor (s); }
Коли ми отримали потрібну кількість класів (інтервалів) за формулою Стерджеса, настає час рознести дані масиву по класах. Такі дані називаються варіантами (в од. Числі - варіáнта ). Зробимо ми це за допомогою функції Allocate наступним чином:
void Allocate (double & data [], int n, double & f [], double & b [], int k) {int i, j; double t, c; t = data [ArrayMinimum (data)]; t = t> 0? t * 0.99: t * 1.01; c = data [ArrayMaximum (data)]; c = c> 0? c * 1.01: c * 0.99; c = (ct) / k / 2; b [0] = t + c; f [0] = 0; for (i = 1; i <k; i ++) {b [i] = b [i - 1] + c + c; f [i] = 0; } For (i = 0; i <n; i ++) for (j = 0; j <k; j ++) if (data [i]> b [j] -c && data [i] <= b [j] + c) {f [j] ++; break; }}
Як можна помітити, функція приймає масив вихідних варіант (data), його довжину (n), число класів (k) і розподіляє варіанти в якийсь конкретний клас f [i] масиву f, де b [i] - це середина класу f [i]. Після цього дані для гістограми готові.
Гістограму будемо відображати за допомогою інструментів, описаних у згаданій раніше статті . Для цього я написав функцію histogramSave, яка і виведе нас гистограмму для досліджуваного ряду в форматі HTML. Функція приймає 2 аргументи: масив класів (f) і масив центрів класів (b).
Як приклад я створив гистограмму для абсолютних різниць максимумів і мінімумів 500-та барів пари EURUSD чотиригодинного тайм-фрейму в пунктах за допомогою скрипта volatilityTest.mq5.
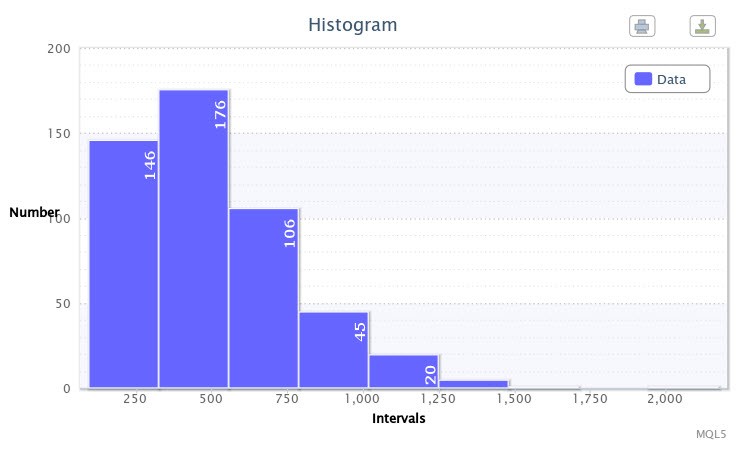
Малюнок 1. Гістограма даних (абсолютна волатильність пари EURUSD H4)
Як видно на графіку (Рис. 1), в перший клас потрапило 146 варіант, у другій - 176 варіант і т.д. Функція гістограми - дати візуальне уявлення про емпіричному розподілі досліджуваної вибірки.
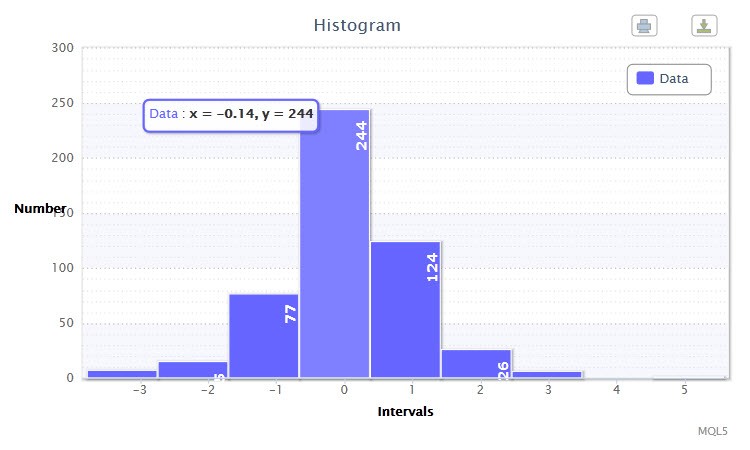
Малюнок 2. Гістограма даних (стандартизовані прибутковості пари EURUSD H4)
На іншому графіку (рис.2) представлені стандартизовані логарифмічні прибутковості 500-та барів пари EURUSD чотиригодинного таймфрейма. Як можна помітити, найбільш представницькими класами стали четвертий і п'ятий, в які потрапило 244 і 124 варіанти відповідно. Гістограма побудована за допомогою скрипта returnsTest.mq5.
Отже, гістограма дозволяє нам вибрати той закон розподілу, параметри якого будуть оцінюватися в подальшому. Якщо візуально не так очевидно, якого розподілу віддати перевагу, то можна оцінювати параметри декількох теоретичних розподілів.
По виду обидва розглянутих розподілу не схожі на нормальні, особливо перший. Але давайте не будемо довіряти візуалізації, а перейдемо до цифр.
2.3 Гіпотеза про нормальність
Традиційно, спочатку вирішується і тестується припущення (гіпотеза) про те, чи є досліджуване розподіл нормальним. Така гіпотеза називається основний. Одним з найпопулярніших методів, які перевіряють нормальність вибірки, є Тест Харки-Бера .
Алгоритм його не самий складний, але досить об'ємний зважаючи на наявність апроксимації. Є кілька версій алгоритму на мові С ++ та інших. Однією з найбільш вдалих і перевірених є версія, що знаходиться в крос-платформної бібліотеці чисельного аналізу ALGLIB . Її автор [Бочканов С.А.] виконав величезну роботу, зокрема щодо складання таблиці квантилів тесту . Я лише тільки трохи її обробив під потреби MQL5 .
Основна функція jarqueberatest виглядає так:
void jarqueberatest (double & x [], double & p) {int n = ArraySize (x); double s; p = 0 .; if (n <5) {p = 1.0; return; } Jarquebera_jarqueberastatistic (x, n, s); p = jarquebera_jarqueberaapprox (n, s); }
Вона обробляє вихідну вибірку даних (x) і повертає р-значення , Тобто величину, що характеризує ймовірність відхилити нульову гіпотезу, якщо насправді нульова гіпотеза вірна.
У тілі функції є ще 2 допоміжні функції. Перша функція - jarquebera_jarqueberastatistic - розраховує статистику Харки-Бера , А друга - jarquebera_jarqueberaapprox - безпосередньо пі-значення. Потрібно зауважити, що остання функція, в свою чергу, задіє допоміжні функції, пов'язані з апроксимацією, яких в алгоритмі майже 30.
Отже, давайте спробуємо протестувати наші вибірки на нормальність. Скористаємося скриптом returnsTest.mq5, який обробить вибірку стандартизованих доходностей пари EURUSD H4.
Як і очікувалося, тест показав, що ймовірність відкинути вірну нульову гіпотезу дорівнює 0.0000. Тобто розподіл цієї вибірки не відноситься до сімейства нормальних. Щоб обробити вибірку абсолютної волатильності пари EURUSD, запустимо скрипт volatilityTest.mq5. Результат буде аналогічний - розподіл не є нормальне.
3. Підгонка розподілу
У математичній статистиці є кілька методів, які дозволяють порівнювати емпіричне розподіл з нормальним. Найбільша проблема полягає в тому, що параметри нормального розподілу нам невідомі і є припущення, що досліджувані дані не показують нормальності розподілу.
Тому доводиться користуватися непараметричних тестами, а невідомі параметри заповнювати оцінками, отриманими з емпіричного розподілу.
3.1 Оцінка і тестування
Одним з найпопулярніших, а головне відповідних, тестів в даній ситуації є χ2-тест . Він заснований на критерії згоди Пірсона .
Провести цей тест нам допоможе функція chsone:
void chsone (double & f [], double & ebins [], double & df, double & chsq, double & prob, const int knstrn = 1) {CGamma gam; int j, nbins = ArraySize (bins), q, g; double temp; df = nbins-knstrn; chsq = 0,0; q = nbins / 2; g = nbins- 1; for (j = 0; j <nbins / 2; j ++) {if (ebins [j] <0.0 || (ebins [j] == 0. && bins [j]> 0.)) Alert ( "Bad expected number in chsone! "); if (ebins [j] <= 5.0) {--df; ebins [j + 1] + = ebins [j]; bins [j + 1] + = bins [j]; } Else {temp = bins [j] -ebins [j]; chsq + = pow (temp; 2) / ebins [j]; }} For (j = nbins- 1; j> nbins / 2- 1; j--) {if (ebins [j] <0.0 || (ebins [j] == 0. && bins [j]> 0. )) Alert ( "Bad expected number in chsone!"); if (ebins [j] <= 5.0) {--df; ebins [j- 1] + = ebins [j]; bins [j- 1] + = bins [j]; } Else {temp = bins [j] -ebins [j]; chsq + = pow (temp; 2) / ebins [j]; }} If (df <1) df = 1; prob = gam.gammq (0.5 * df, 0.5 * chsq); }
З лістингу видно, що використовується екземпляр класу CGamma, що представляє неповну гамма-функцію, включений, як і всі згадані розподілу в файл Distribution_class.mqh. Ще потрібно сказати, що масив очікуваних частот (ebins) ми отримаємо за допомогою функцій estimateDistribution і expFrequency.
Тепер потрібно підібрати числові параметри, які входять в аналітичну формулу теоретичного розподілу. Число параметрів залежить від конкретного розподілу. Так, в нормальному розподілі їх два, в показовому - один і т.д.
Зазвичай при знаходженні параметрів розподілу використовують такі методи точкової оцінки параметрів як: метод моментів, квантилів і метод максимальної правдоподібності. Перший є більш простим, так як передбачає, що вибіркові оцінки (матожіданіє, дисперсія, асиметрія і т.д.) повинні збігатися з генеральними.
Давайте на прикладі спробуємо підібрати теоретичний розподіл для нашої вибірки. Візьмемо ряд стандартизованих доходностей пари EURUSD H4, для якого ми вже відображали гистограмму.
По першому враженню, нормальний розподіл для цього ряду не підходить, тому що спостерігається надлишковий коефіцієнт ексцесу. Давайте спробуємо застосувати для порівняння інший розподіл.
Отже, при запуску вже відомого скрипта returnsTest.mq5 спробуємо вибрати такий розподіл, як Hypersec. Крім усього іншого скрипт оцінить і виведе параметри обраного розподілу за допомогою функції estimateDistribution і відразу ж проведе χ2-тест . Параметри для вибраного розподілу виявилися такими:
Hyperbolic Secant distribution: X ~ HS (-0.00, 1.00);
а результати тесту такими:
"Статистика Хі-квадрат: 1.89; ймовірність відкинути вірну нульову гіпотезу: 0.8648"
Потрібно відзначити, що розподіл підібрано дуже вдало, так як величина χ2-статистики вельми незначна.
На додаток, за допомогою функції histogramSaveE буде побудована подвійна гістограма для фактичних і очікуваних частостей (Частость-частота, виражена в частках або відсотках) стандартизованих доходностей (Рис. 3). На ній помітно, що стовпчики практично дублюють один одного. Що говорить про успішну підгонці.
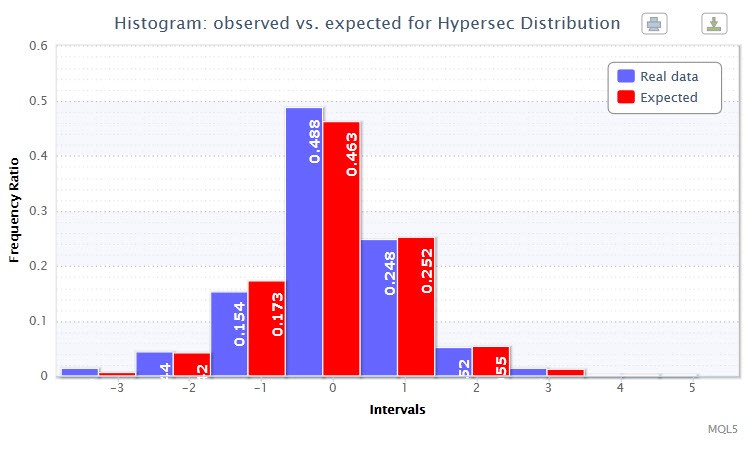
Малюнок 3. Гістограма фактичних і очікуваних частостей (стандартизовані прибутковості пари EURUSD H4)
Проведемо аналогічну процедуру для даних волатильності за допомогою вже знайомого скрипта volatilityTest.mq5.
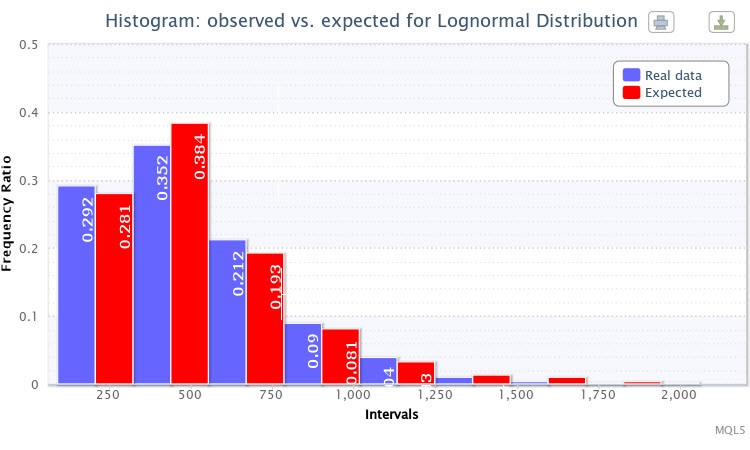
Малюнок 4. Гістограма фактичних і очікуваних частостей (абсолютна волатильність пари EURUSD H4)
Я вибрав логнормальний розподіл для тестування Lognormal. Після цього отримав таку оцінку параметрів:
Lognormal distribution: X ~ Logn (6.09, 0.53);
а результати тесту такими:
"Статистика Хі-квадрат: 6.17; ймовірність відкинути вірну нульову гіпотезу: 0.4040"
Для цього емпіричного розподілу теж вельми вдало підібрано теоретичне. Таким чином, можна вважати, що нульову гіпотезу відкинути не можна (при стандартному рівні значущості p = 0.05). На Рис. 4 можна побачити, що стовпчики очікуваних і фактичних частостей також дуже схожі один на одного.
Давайте тепер згадаємо, що у нас ще є можливість генерувати вибірку випадкових величин з деякого розподілу з заданими параметрами. Для використання ієрархії класів, пов'язаних з такою операцією, я написав скрипт randomTest.mq5.
При його запуску потрібно буде ввести такі параметри, проілюстровані на Рис. 5.
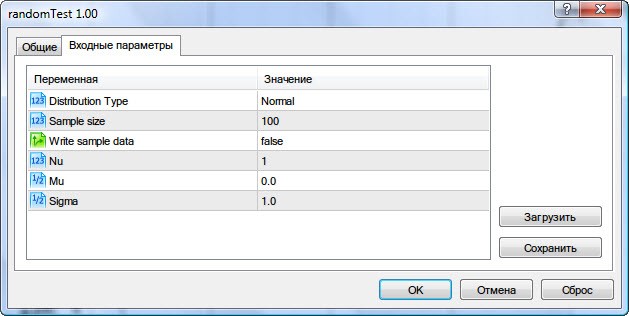
Малюнок 5. Вхідні параметри скрипта randomTest.mq5
Тут можна вибрати тип розподілу (Distribution Type), число випадкових величин вибірки (Sample Size), можливість зберегти вибірку (Write sample data), параметр Nu (для розподілу Стьюдента), параметр Mu і Sigma.
Якщо задати для Write sample data значення true, то скрипт збереже вибірку випадкових величин до призначених для користувача параметрами в файл Randoms.csv. В іншому випадку він буде зчитувати дані вибірки з цього файлу і потім проводити статистичні тести.
Для деяких розподілів, у яких параметри Mu і Sigma відсутні, я привожу таблицю параметричного відповідності полям у вікні запуску скрипта.
Розподіл Перший параметр в розподілі Другий параметр в розподілі Logistic alph -> Mu bet -> Sigma Exponential lambda -> Mu - Gamma alph -> Mu bet -> Sigma Beta alph -> Mu bet -> Sigma Laplace alph -> Mu bet -> Sigma Binomial n -> Mu pe -> Sigma Poisson lambda -> Mu -
Так, якщо вибрати розподіл Poisson, то параметр lambda введемо через поле Mu і т.д.
Скрипт не оцінює параметри розподілу Стьюдента з огляду на те, що воно використовується в абсолютній більшості випадків лише для деяких статистичних процедур: для точкового оцінювання, побудови довірчих інтервалів і тестування гіпотез, що стосуються невідомого середнього статистичної вибірки з нормального розподілу.
Як приклад я запустив скрипт для нормального розподілу з параметрами X ~ Nor (3.50, 2.77) при Write sample data = true. Спочатку скрипт згенерував вибірку. Повторний його запуск при Write sample data = false побудував таку гістограму, як відображено на Рис.6.
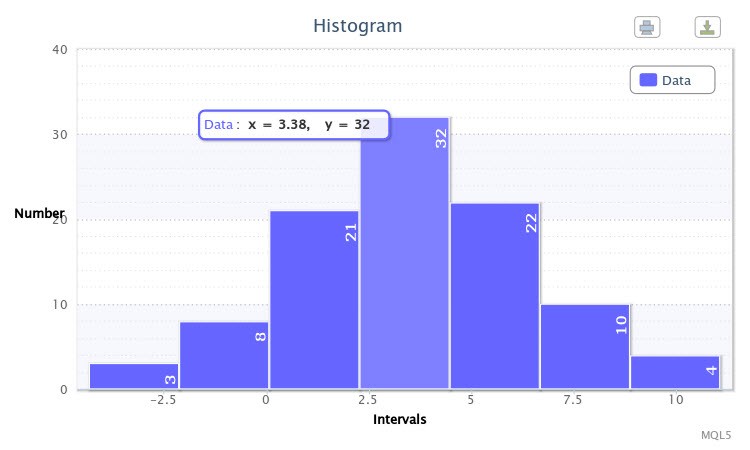
Малюнок 6. Вибірка випадкових величин X ~ Nor (3.50,2.77)
Інша інформація, яка була виведена в вікно терміналу:
Тест Харки-Бера: "Тест Харки-Бера: ймовірність відкинути вірну нульову гіпотезу дорівнює 0.9381";
Оцінка параметрів: Normal distribution: X ~ Nor (3.58, 2.94);
Результати Хі-квадрат тесту: "Статистика Хі-квадрат: 0.38; ймовірність відкинути вірну нульову гіпотезу: 0.9843".
І в підсумку була відображена ще одна подвійна гістограма фактичних і очікуваних частостей для вибірки (Рис. 7).
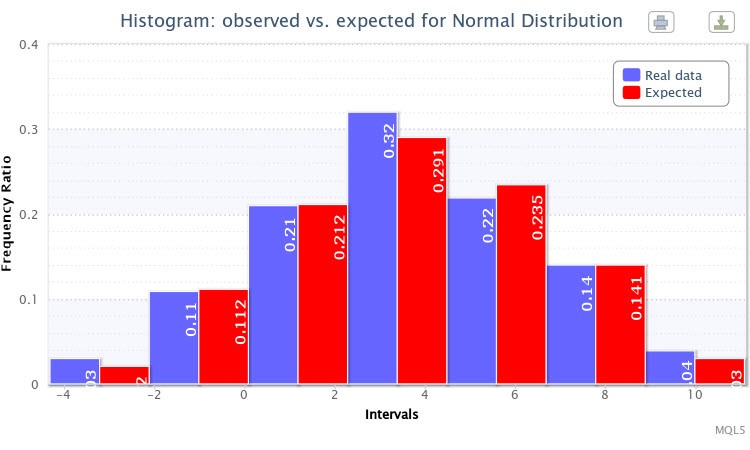
Малюнок 7. Гістограма фактичних і очікуваних частостей для X ~ Nor (3.50,2.77)
Загалом, генерація зазначеного розподілу пройшла добре.
Ще я написав скрипт fitAll.mq5, який працює аналогічно скрипту randomTest.mq5. Різниця лише в тому, що в першому є функція fitDistributions. Я поставив для неї таку задачу: підігнати під вибірку випадкових величин всі наявні розподілу і провести статистичний тест.
Не завжди якесь розподіл можна підігнати до вибірці через параметричного невідповідності, тому в терміналі можуть з'являтися рядки, що оцінка неможлива, наприклад "Beta distribution can not be estimated!".
Ще, я вирішив, що цей скрипт буде візуалізувати статистичні результати у вигляді невеликого HTML-звіту, приклад якого є в статті Графіки і діаграми в форматі HTML (Рис. 8).
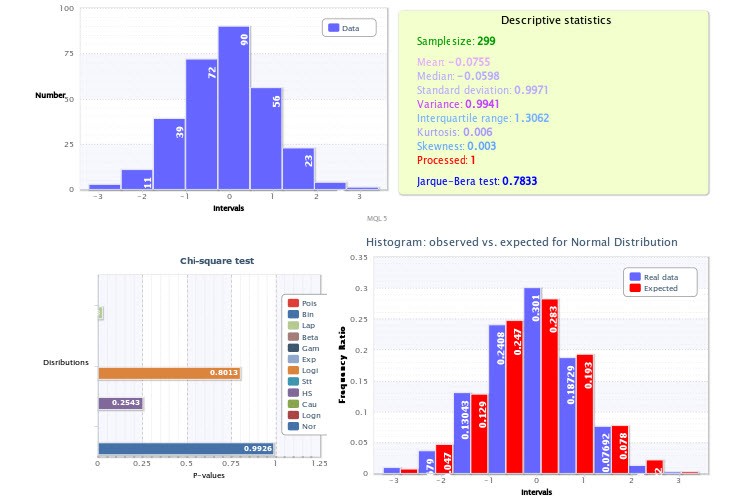
Малюнок 8. Статистичний звіт оцінки вибірки
У верхній лівій чверті показана звичайна гістограма вибірки, а в правій - описові статистики та результат тесту Харки-Бера , Де змінна Processed означає, що при значенні 1 були видалені викиди, а при значенні 0 - їх не було.
У нижній лівій чверті наведені пі-значення χ2-тесту для кожного підібраного розподілу. Тут, найкраще з точки зору підгонки стало нормальний розподіл (p = 0.9926). Тому для нього була побудована гістограма фактичних і очікуваних частостей в нижній правій чверті.
Поки в моїй галереї трохи розподілів. Але при великому числі розподілів такий скрипт заощадить багато часу.
Тепер, коли ми точно знаємо параметри розподілів досліджуваних вибірок, можна перейти до імовірнісних міркувань.
3.2 Вірогідність значень випадкових величин
В статті про теоретичні розподілу я приводив скрипт continuousDistribution.mq5 як приклад. З його допомогою спробуємо відобразити будь-який для нас цікавий закон розподілу з відомими параметрами.
Так, для даних волатильності введемо раніше отримані параметри логнормального розподілу (Mu = 6.09, Sigma = 0.53), виберемо тип розподілу Lognormal і вид cdf (Рис.9).
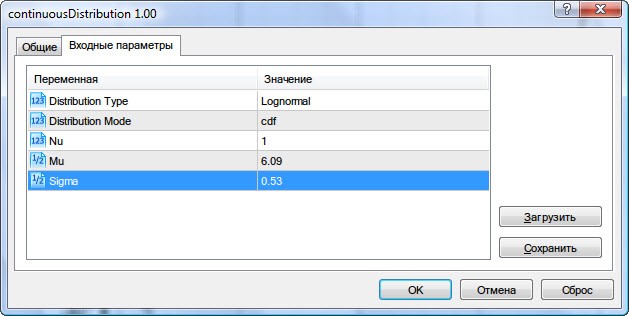
Малюнок 9. Параметри логнормального розподілу X ~ Logn (6.09,0.53)
Після цього скрипт відобразить нам функцію розподілу для нашої вибірки. Вона буде мати вигляд, показаний на Рис. 10.
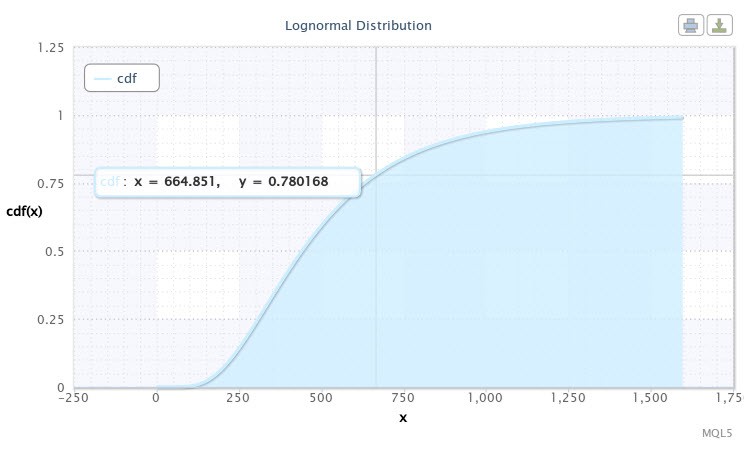
Малюнок 10. Функція розподілу для X ~ Logn (6.09,0.53)
На графіку ми бачимо, що курсор наведений на точку, координати якої приблизно рівні [665; 0.78]. Це означає, що з імовірністю 78% волатильність пари EURUSD H4 не перевищить 665 пп. Така інформація може виявитися дуже цінною для розробника експерта. Природно, що значення на кривій можна взяти і інші, пересуваючи курсор.
Припустимо, що нас цікавить ймовірність того, що величина волатильності виявиться в проміжку між 500-ми пп і 750-ма пп. Для цього потрібно провести таку операцію:
cdf (750) - cdf (500) = 0.84 - 0.59 = 0.25.
Таким чином, в чверті випадків волатильність пари коливається між 500-ми пп і 750-ма пп.
Давайте ще раз запустимо скрипт з тими ж параметрами розподілу, тільки як вид закону розподілу вкажемо sf. Функція надійності (виживання) покаже нам наступну картину (Рис.11).
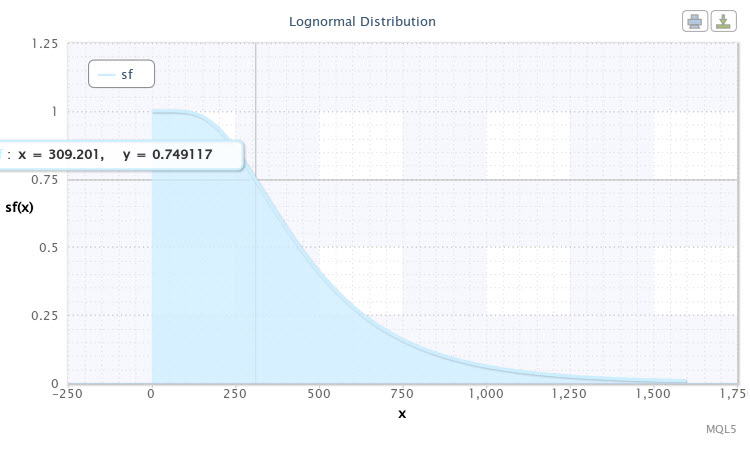
Малюнок 11. Функція надійності для X ~ Logn (6.09,0.53)
Виділену точку на графіку кривої можна трактувати наступним чином: майже з ймовірністю 75% ми можемо очікувати, що волатильність пари складе 310 пп. І чим нижче будемо опускатися по кривій, тим менше буде вірогідність зростання волатильності. Так, волатильність більше 1000 пп вже можна буде віднести до рідкісних подій, тому що ймовірність її появи складе менше 5%.
Для вибірки стандартизованих доходностей, як втім і для інших вибірок, можна побудувати аналогічні криві розподілу. Вважаю, що методика в загальному і цілому ясна.
Висновок
Потрібно відзначити, що пропоновані аналітичні висновки не є абсолютно успішними, тому що самі ряди мають властивість змінюватися. Правда це не стосується, наприклад, рядів логарифмічних доходностей. Але в цій статті я і не ставив завданням оцінювати самі методи. Пропоную зацікавленому читачеві висловлюватися з цієї проблематики.
Вважаю важливим відзначити необхідність відношення до ринку, ринкових інструментів і торговим експертам з позиції ймовірності. Такий підхід я і спробував продемонструвати. Сподіваюся, що тема зацікавить читача, що виллється в конструктивну дискусію.
Розташування файлів:
# Файл Шлях Опис 1 Distribution_class.mqh% MetaTrader% \ MQL5 \ Include Галерея класів розподілів 2 DistributionFigure_class.mqh% MetaTrader% \ MQL5 \ Include Класи графічного відображення розподілів 3 Random_class.mqh% MetaTrader% \ MQL5 \ Include Класи генерації вибірки випадкових чисел 4 ExpStatistics_class.mqh% MetaTrader% \ MQL5 \ Include Клас і функції оцінок статистичних характеристик 5 volatilityTest.mq5% MetaTrader% \ MQL5 \ Scripts Скрипт оцінки вибірки волатильності EURUSD H4 6 returnsTest.mq5% MetaTrader% \ MQL5 \ Scripts Скрипт оцінки вибірки доходностей EURUSD H4 7 randomTest.mq5% MetaTrader% \ MQL5 \ Scripts Скрипт оцінки вибірки випадкових величин 8 fitAll.mq5% MetaTrader% \ MQL5 \ Scripts Скрипт підгонки і оц нки всіх розподілів 9 Volat.csv% MetaTrader% \ MQL5 \ Files Файл даних вибірки волатильності EURUSD H4 10 Returns_std.csv% MetaTrader% \ MQL5 \ Files Файл даних вибірки доходностей EURUSD H4 11 Randoms.csv% MetaTrader% \ MQL5 \ Files Файл даних вибірки випадкових величин 12 Histogram.htm% MetaTrader% \ MQL5 \ Files HTML-графік гістограми вибірки 13 Histogram2.htm% MetaTrader% \ MQL5 \ Files HTML-графік подвійний гістограми вибірок 14 chi_test.htm% MetaTrader% \ MQL5 \ Files Статистичний HTML- звіт оцінки вибірки 15 dataHist.txt% MetaTrader% \ MQL5 \ Files Дані для відображення гістограми вибірок 16 dataHist2.txt% MetaTrader% \ MQL5 \ Files Дані для відображення подвійний гістограми вибірок 17 dataFitAll.txt% MetaTrader% \ MQL5 \ Files Дані для відображення HTML-звіту 18 highcharts.js% MetaTrader% \ MQL5 \ Files JavaScript-бібліотека інтерактивних графіків 19 jquery.min.js% MetaTrader% \ MQL5 \ Files JavaScript-бібліотека 20 ReturnsIndicator.mq5% MetaTrader% \ MQL5 \ Indicators Індикатор логарифмічних доходностей
Використовувана література:
Ch. Walck, Hand-book on Statistical Distributions for Experimentalists, University of Stockholm Internal Report SUF-PFY / 96-01
Numerical Recipes: The Art of Scientific Computing, Third Edition William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery, Cambridge University Press: 2007. - тисяча двісті п'ятьдесят-шість pp.
STATISTICS Methods and Applications Book By Pawel Lewicki and Thomas Hill, StatSoft, Inc .; 1 edition (November 2005), 800 pages.
Боровков А.А. Математична статистика. - Підручник. - М .: Наука. Головна редакція фізико-математичної літератури, 1984. - 472 с.
Булашев С.В. Статистика для трейдерів. - М .: Компанія Супутник +, 2003. - 245 с.
Вадзінську Р.Н. Довідник по імовірнісним розподілом. - СПб .: Наука, 2001. - 295 с., Іл. 116.
Гайдишев І. Аналіз і обробка даних: спеціальний довідник - СПб: Пітер, 2001. - 752 с .: іл.
Гнеденко Б.В. Курс теорії ймовірності: Підручник. Вид. 8-е, испр. и доп. - М .: Едіторіал УРСС, 2005. - 448 с.
Іглін С. П. Теорія ймовірностей та математична статистика на базі MATLAB: Навч. посіб. - Харків: НТУ "ХПІ", 2006. - 612 c. - Рос. мовою.
Івченко Г.І., Медведєв Ю.І. Математична статистика: Учеб. посібник для втузів. - М .: Вища. шк., 1984. - 248 с., іл.
Кібзун А.І., Горяїнова О.Р. - Теорія ймовірностей і математична статистика. Базовий курс з прикладами і завданнями
Письмовий Д.Т. Конспект лекцій з теорії ймовірностей і математичній статистиці. - М .: Айріс-прес, 2004. - 256 с .
NIST / SEMATECH e-Handbook of Statistical Methods
xycoon.com